How Does SAFER Work?
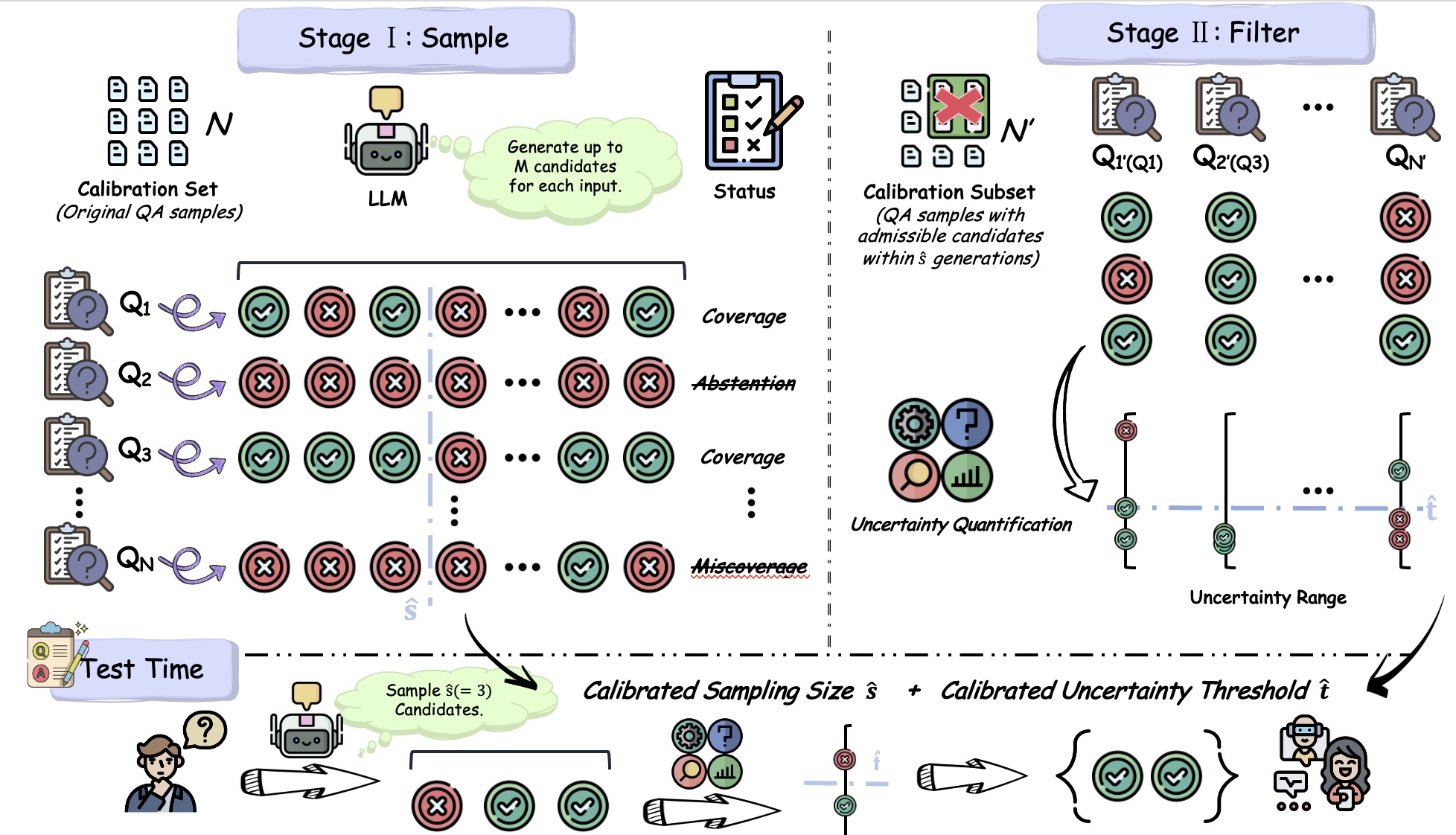
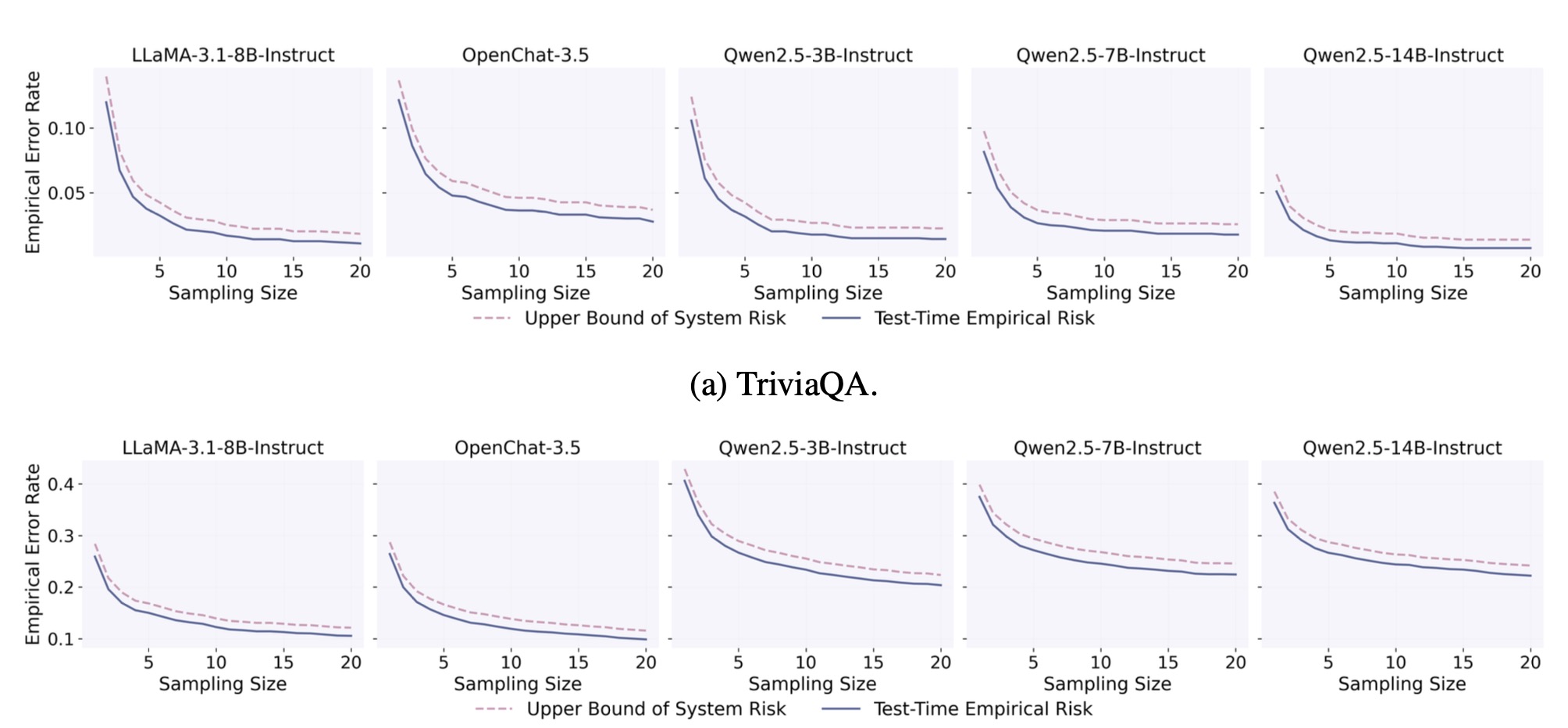
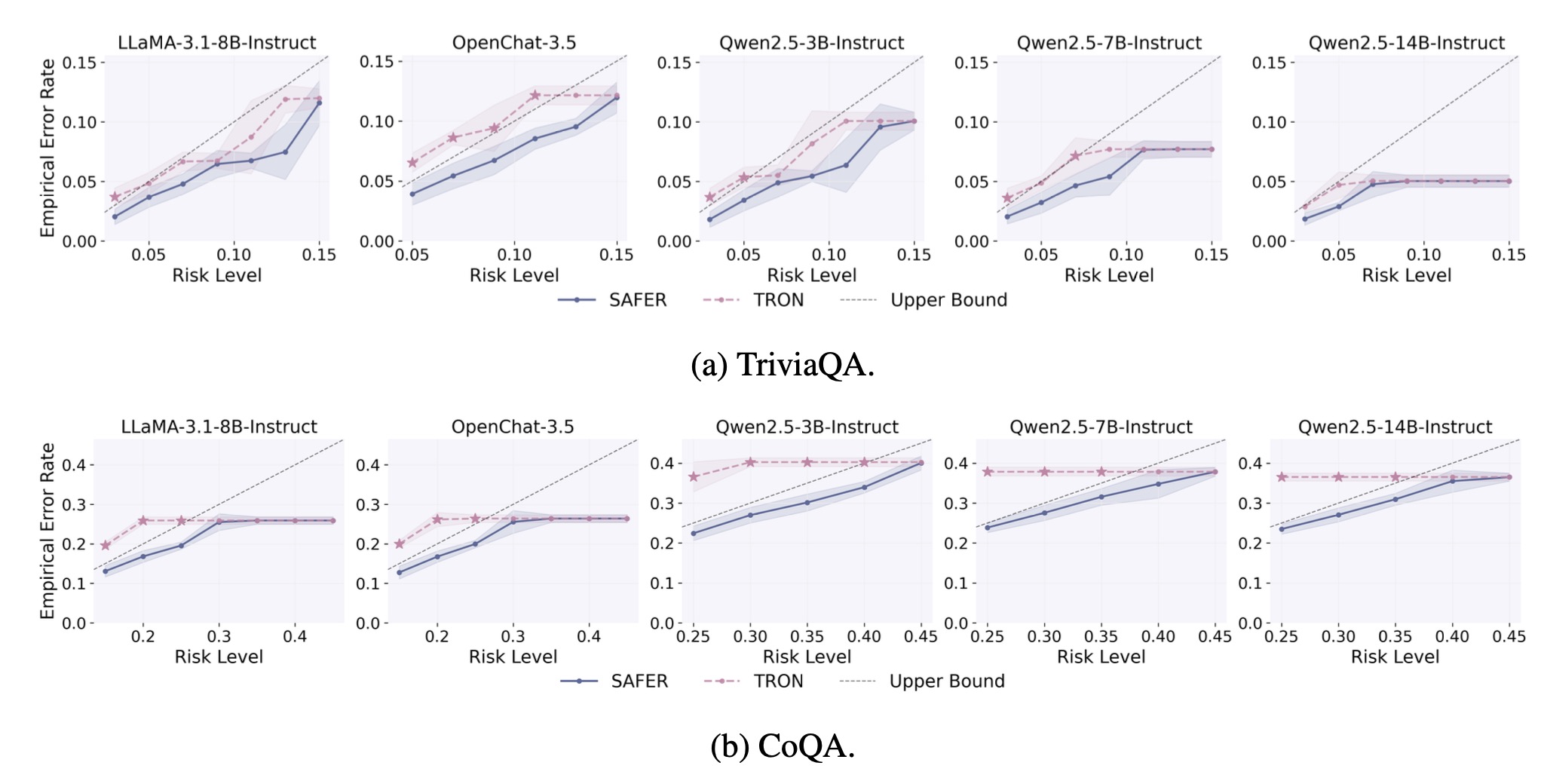
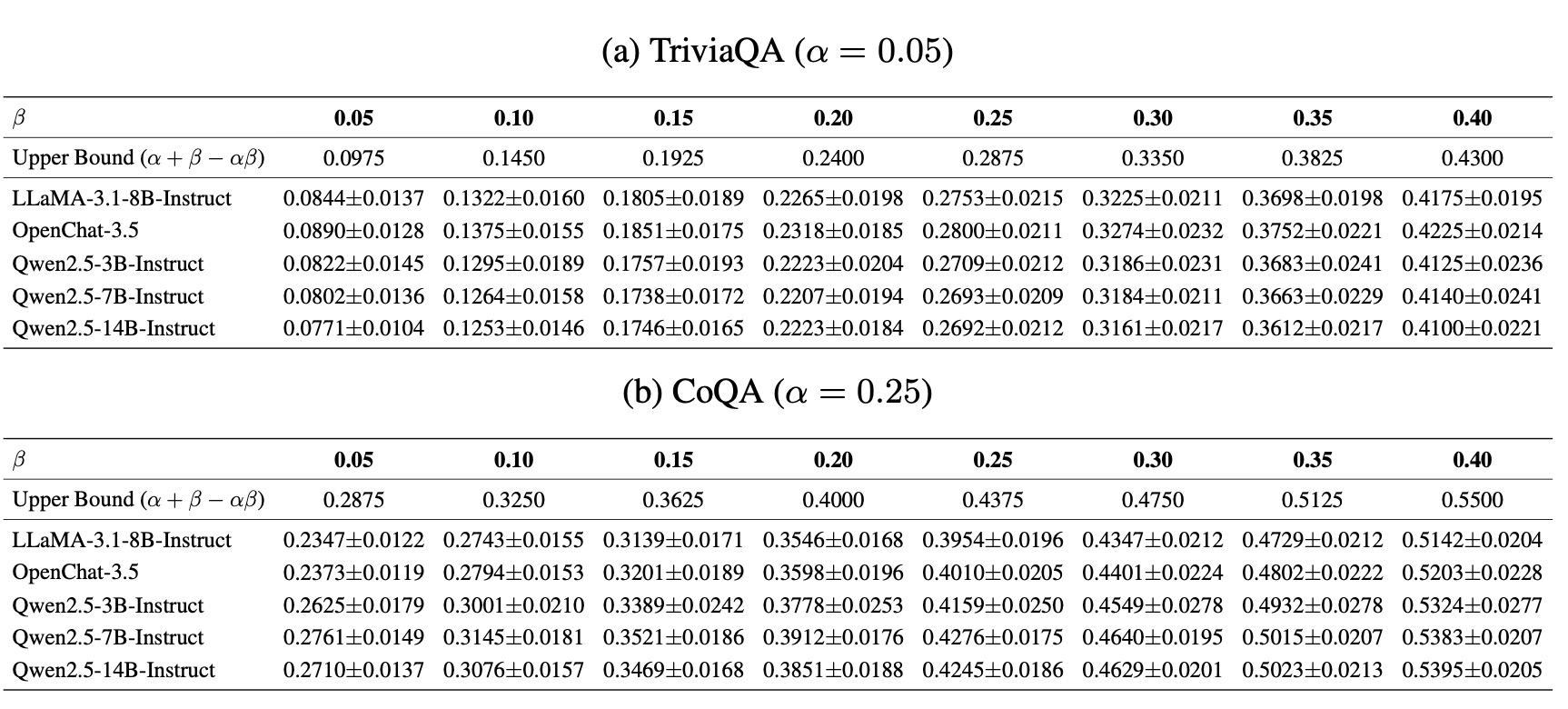
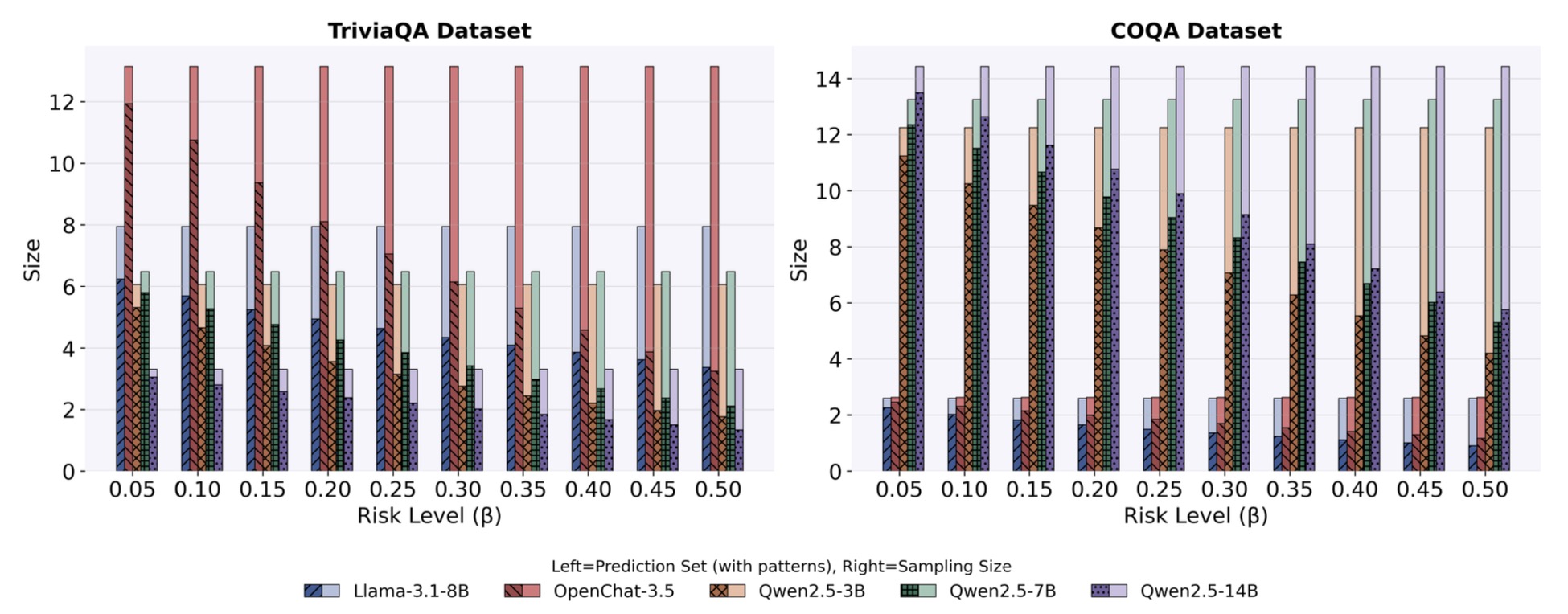
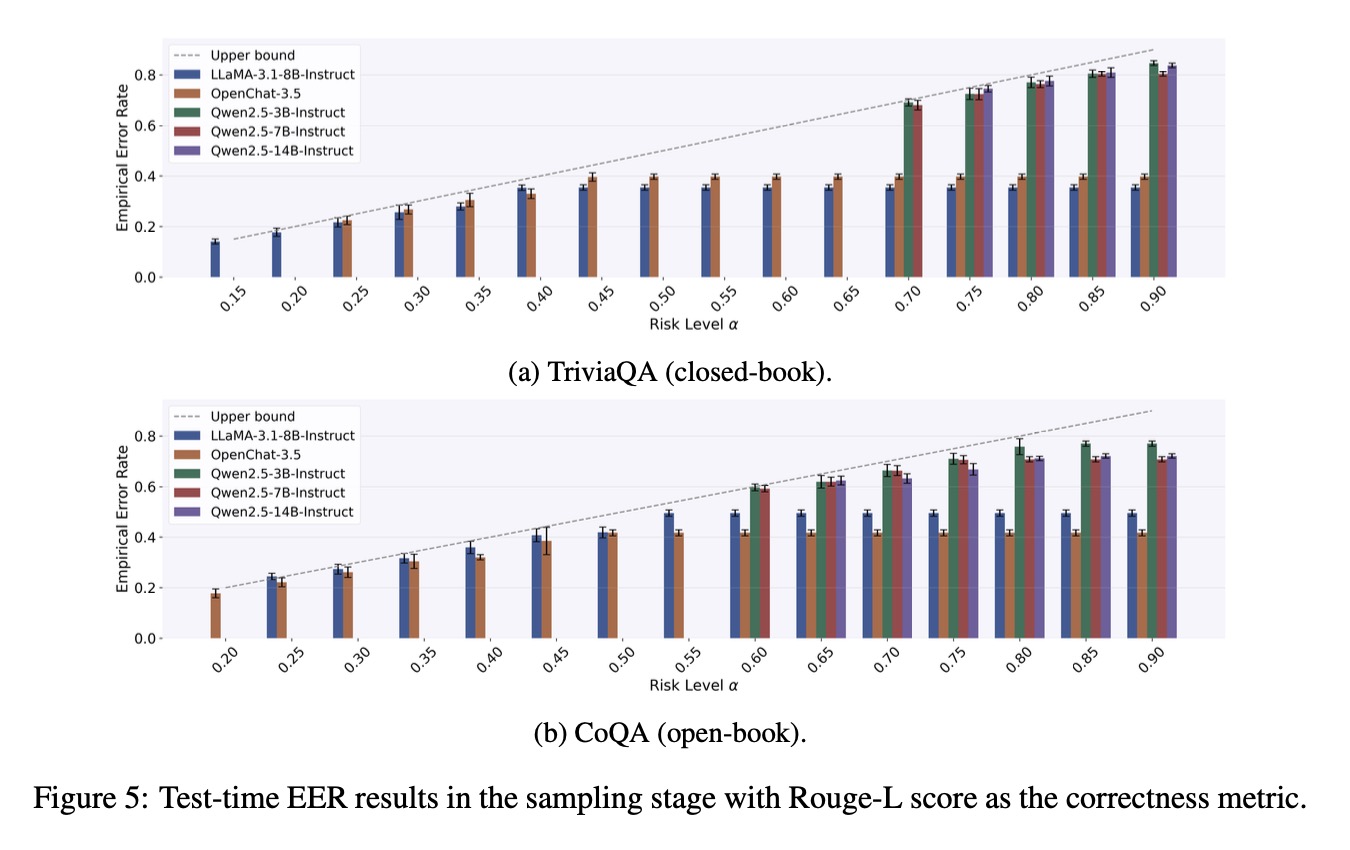
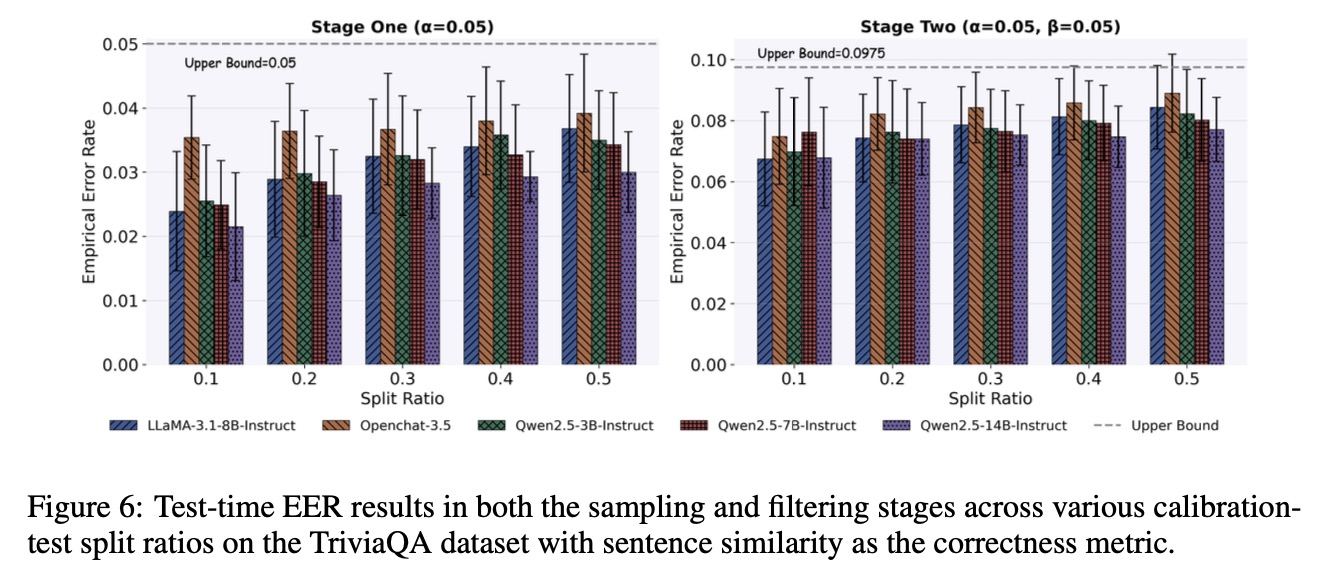
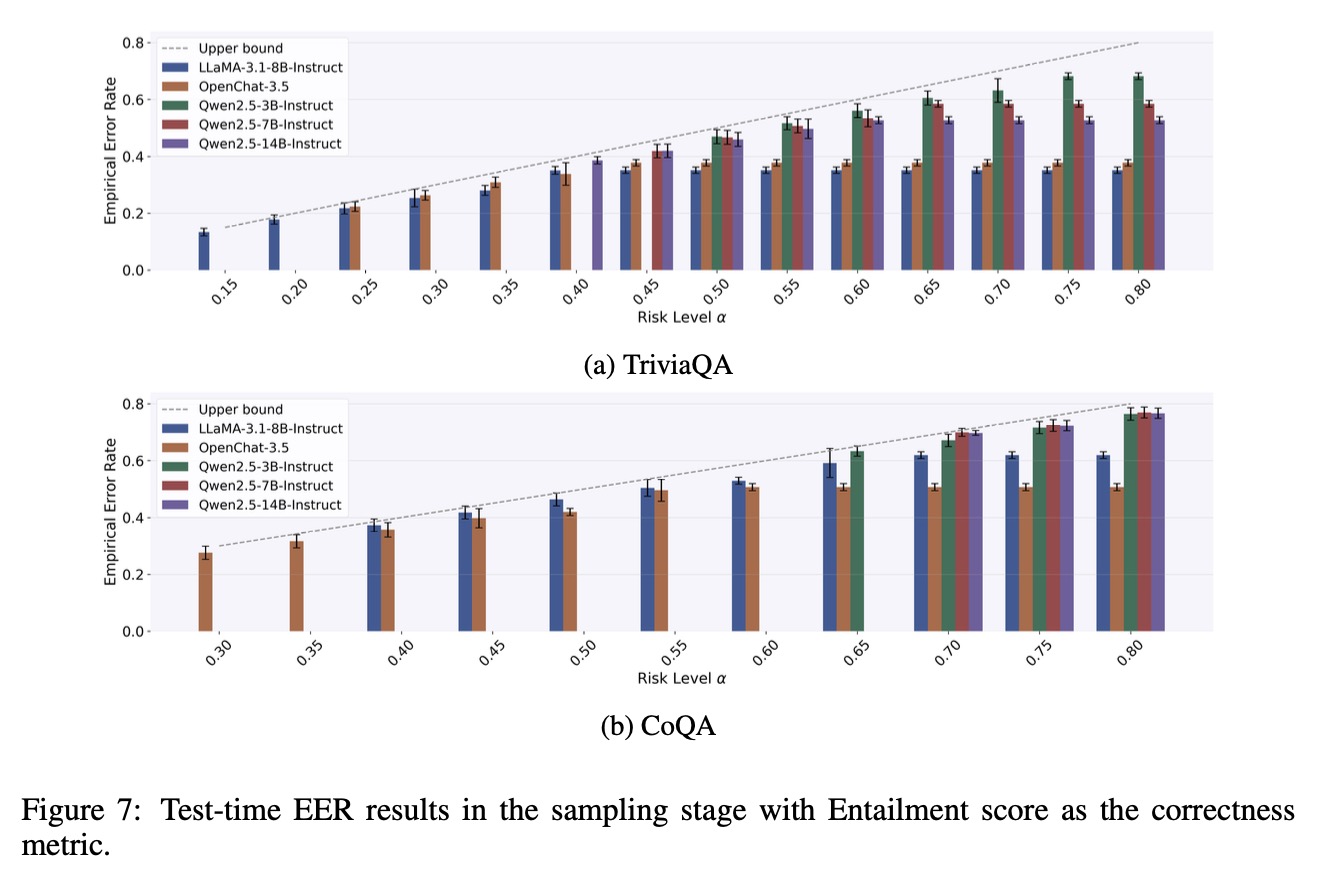
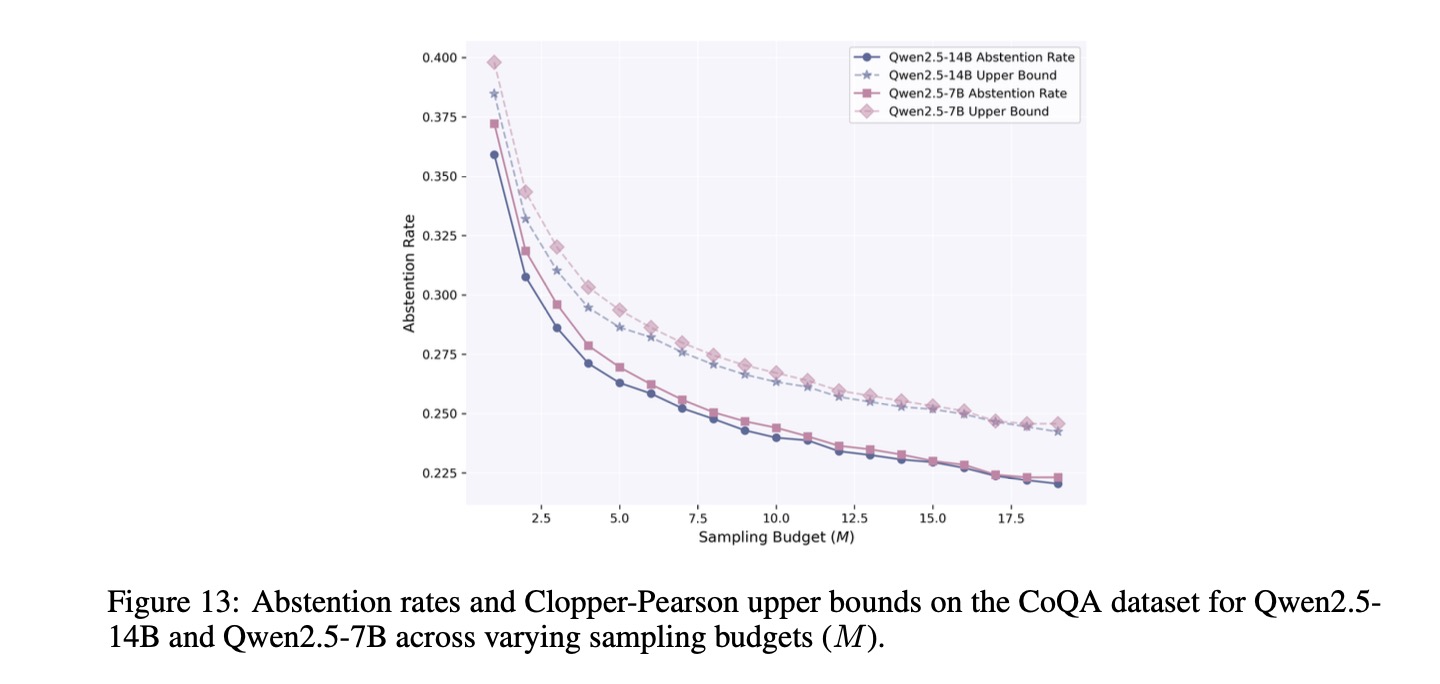
Overview of SAFER's calibration and test-time process. In Stage I, we derive a statistically valid minimum sample budget \(\hat{s}\) that can strictly control the test-time risk of the candidate set of size \(\hat{s}\) not covering correct answers. In Stage II, we employ the calibration instances, which can obtain admissible answers within \(\hat{s}\) samples, to calibrate a threshold \(\hat{t}\). This threshold filters out unreliable answers in the candidate set while still constraining the miscoverage risk of the final prediction set.